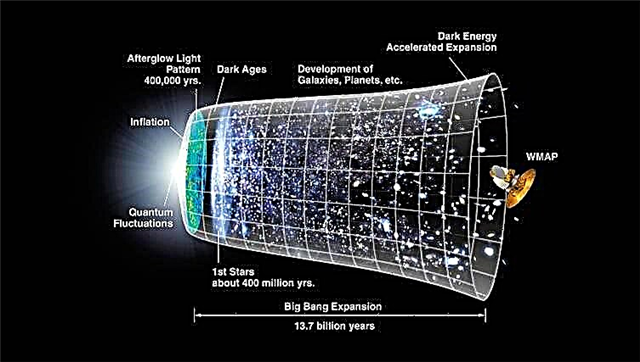
뉴욕-2,000 년 이상 존재했지만 무한의 개념은 수학자, 물리학 자 및 철학자들에게 수수께끼로, 때로는 도전적인 아이디어로 견뎌 왔습니다. 무한대가 실제로 존재합니까, 아니면 우리 상상력의 일부일까요?
과학자와 수학자 패널이 모여 금요일 (5 월 31 일) 무한 과학 개념을 둘러싼 심오한 질문과 논란에 대해 논의하며, 매년 과학 축제 인 세계 과학 축제의 일환으로 세계 과학 축제의 일환으로 개최됩니다.
버클리 캘리포니아 대학교의 수학자 인 윌리엄 휴 우딘 (William Hugh Woodin)은 무한대와 관련된 추상적 문제를 풀기 어려운 점 중 하나는 이러한 문제가 더 확립 된 수학적 이론을 넘어선다는 점이라고 말했다.
우딘은“수학이 안정된 섬에 사는 것처럼 일종의 기초가되었다”고 말했다. "그럼 거기에 야생의 땅이 있습니다. 그것은 무한대입니다."
모든 것이 시작된 곳
기원전 490 년부터 살았던 엘리아의 제노 (Zeno)라는 철학자. 기원전 430 년에 무한의 아이디어를 도입 한 것으로 인정됩니다.
이 개념은 아리스토텔레스를 포함한 고대 철학자들에 의해 연구되어 유한 한 물리적 세계에 무한이 존재할 수 있는지에 대해 의문을 제기했다고 캘리포니아 클래어 몬트의 클레어몬트 클레어몬트 대학교에있는 클레어몬트 신학 대학원의 필리 클레이튼은 토마스 아퀴나스를 포함한 신학자 인간과 신과 자연계의 관계를 설명하기 위해 무한을 사용했습니다.
1870 년대에 게오르그 캔터 (Georg Cantor)라는 독일의 수학자가 고정 이론으로 알려진 분야에서 작업을 개척했습니다. 집합 이론에 따르면, 분수 또는 소수 성분이없는 숫자 (예 : 1, 5, -4)는 계산할 수있는 무한 집합을 구성합니다. 반면 정수, 분수 및 소위 비이성 수 (예 : 제곱근 2)를 포함하는 실수는 셀 수없는 무한 세트의 일부입니다.
이로 인해 Cantor는 다양한 유형의 무한대에 대해 궁금해했습니다.
"이제 두 종류의 무한대가있을 경우, 셀 수있는 종류와이 연속적인 종류가 더 큽니다. 다른 무한대가 있습니까? 그들 사이에 끼인 무한대가 있습니까?" 뉴욕 이타카 코넬 대학의 수학자 Steven Strogatz가 말했다.
Cantor는 정수 세트와 실수 사이에 무한대가 없다고 믿었지만 결코 그것을 증명할 수 없었습니다. 그러나 그의 진술은 연속 가설로 알려졌으며, 캔터의 발자취에서 문제를 해결 한 수학자들은 고정 이론가로 분류되었다.
넘어서 탐험
Woodin은 이론가로, 연속체 가설을 풀기 위해 평생을 보냈습니다. 현재까지 수학자들은 Cantor의 가정을 증명하거나 반증 할 수 없었습니다. 문제의 일부는 무한대 유형이 두 개 이상이라는 아이디어가 너무 추상적이라고 Woodin은 말했다.
"연속 가설을 측정하고 나가기 위해 구축 할 수있는 위성은 없다"고 그는 설명했다. "우리 주변에는 우리가 아는 한 연속체 가설이 참인지 거짓인지 판단하는 데 도움이되는 것은 아무것도 없습니다."
Trickier는 여전히 일부 수학자들이 이런 유형의 수학 작업의 관련성을 무시했다는 사실입니다.
스트로 가츠는“이론을 설정 한 사람들은 수학에서도 이상한 일로 우리를 때린다”고 농담했다. 그러나 그는 연속 이론 가설이 거짓으로 판명되면 대수 이론이 모순되는 수학과 물리의 기초를 없애는 것과 같은 방식으로 기본 수학 원리를 근절 할 수 있기 때문에 세트 이론가들에 의해 수행되는 작업의 중요성을 이해한다고 말했다.
스트로 가츠는“우리는 그들이 정말로 깊고 중요한 일을하고 있다는 것을 알고 있습니다. "2 층과 3 층에서 우리 모두가 작업하고있는 기초를 흔들고 있습니다. 그들이 무언가를 엉망으로 만들면 우리 모두에게 도움이 될 수 있습니다."
수학의 미래
그럼에도 불구하고 모든 불확실성에도 불구하고 세트 이론가들에 의해 수행 된 연구는 수학의 기초를 강화시키는 데 기여하는 긍정적 파급 효과를 가질 수 있다고 Woodin은 말했다.
"무한도를 조사하고 성공할 수있는 정도까지 산술의 일관성에 대한 사례를 만든다고 생각한다"고 그는 설명했다. "그것은 약간의 광신적 진술이지만, 무한대가 모순으로 이어지지 않는다면, 유한 한 것이 모순으로 이어지지는 않습니다. 따라서 아마도 모퉁이가 있는지 알아보기 위해 바깥 쪽 범위를 탐색하면 보안."
Strogatz는 무한의 개념을 특징 짓는 역설은 아마도 숫자 pi로 가장 잘 설명 될 것이라고 말했다. 가장 잘 알려진 수학적 상수 중 하나 인 Pi는 원주와 지름의 비율을 나타냅니다. 수많은 응용 분야 중에서 pi를 사용하여 원의 면적을 찾을 수 있습니다.
Strogatz는 "Pi는 일반적으로 실제 숫자입니다. 예측할 수없는 정보가 무한히 많고 동시에 완전히 예측할 수 있습니다"라고 말합니다. "파이가 구현하는 원보다 더 질서가 없습니다. 그것은 질서와 완벽의 상징입니다. 따라서 같은 물체에 내장 된 무한한 수수께끼의이 신비로운 미스터리와 함께 완벽한 예측 성과 질서의 공존은 즐거움의 일부입니다. 우리의 주제와 무한 성 자체에 대해 생각합니다. "